• 작성자: 10기 김지중

본 문서는 Coursera - Convolutional Neural Networks의 1주차 강의 내용에 대한 정리 / 보충 자료다.

1주차 강의는 CNN을 구성하는 핵심 요소인 Convolution의 개념을 중점적으로 다룬다. 이후 padding, stride 등등 CNN에서 쓰이는 용어에 대해 설명하고, Pooling의 개념을 다룬다. 실습 과제는 Convolution layer와 Pooling layer의 구현, 그리고 간단한 CNN 분류기의 구현으로 이루어져있다.

Convolution 연산과 Edge Detection

CNN에서는 각각의 레이어가 이미지에서 feature를 학습한다. 앞단의 layer에서는 가장 저차원의 feature인 edge 등에 대해 학습할 것이고, 레이어를 쌓으면 쌓을 수록 보다 복잡한 형태의 feature를 학습한다. 아래 이미지에서 역시 초반에 edge를 학습한 이후, 중간단에서는 눈, 코, 입 등을, 그리고 뒷단에서는 전체 얼굴의 형체를 학습하는 것을 확인할 수 있다.

강의에서는 edge detection을 통해 기본적인 convolution 연산을 설명한다.

먼저 Vertical Edge Detection이다. 6x6의 이미지에 3x3의 필터를 입히면 4x4의 feature map이 나온다. 이미지 음영 처리된 부분을 한 칸씩 옆으로 / 아래로 옮긴다고 생각하면, feature map이 왜 4x4 차원이 되는지 쉽게 이해할 수 있다. Feature map의 각각의 픽셀 값(?)은 다음과 같은 과정으로 계산된다.

• 위 그림의 파란색 음영과 같이 3x3의 필터를 이미지 위에 덧댄다.
• 이미지의 픽셀값과 필터의 값을 element-wise product한다.
• 그 값들을 모두 더한다.
• 위 예시에서는, 3x3+0x0+1x-1+1x1+5x0+8x-1+2x1+7x0+2x-1을 의미한다.
• 이렇게 이미지-필터간의 element-wise product를 모두 더해주는 연산을 convolution이라 부른다. 연산 기호는 *로 표기한다.

그런데 이게 왜 Vertical Edge Detection일까? 다른 예시를 통해 확인해보자.

위 이미지는 2차원으로 구성되었다. 즉, 흑백의 이미지다. 각 픽셀 값이 클 수록 흰색, 작을 수록 검정색에 가깝다. 위 그림의 왼쪽 매트릭스는 왼쪽 절반은 하얗고, 오른쪽은 까만 이미지를 의미한다. 즉, 이미지 가운데에 수직의 edge가 존재한다. 이 때, 그림 중간과 같은 필터를 통해 convolution 과정을 거치면 오른쪽과 같은 feature map이 나온다. Feature map을 이미지로 표현하면, 가운데 부분이 수직으로 하얗게 표시된다. 즉, 이 하얀 부분은 원래 이미지의 edge를 나타내는 것이다.

위에서 사용된 필터가 의미하는 바는, 왼쪽에 밝은, 오른쪽은 어두운 픽셀이 있을 경우 활성화되는 것이다. 따라서 Feature Map 가운데에 하얗게 Vertical Edge가 탐지된 것이다.

Vertical Edge를 탐지할 수 있다면, Horizontal Edge도 탐지할 수 있을 것이다. 위 처럼, Vertical Edge Detecting Filter를 90도 회전하면 Horizontal Edge Detecting Filter를 얻을 수 있다. 비슷한 방식으로 수직, 수평 뿐만 아니라 45도, 60도 등 다양한 각도의 Edge를 탐지할 수 있다.

이렇게 특정 각도를 학습하기 위하 만든 필터를 hand coded filters라고 부른다. 특정한 Edge를 뽑아내기 위해 연구자가 임의로 필터의 각 값을 지정한 것이다. 뉴럴 네트워크에서는 Backpropagation 등을 통해 각각의 필터 값을 학습한다. 이를 통해 보다 hand coded filter를 이용할 때보다 robust한 학습이 가능하다.

Padding

다음으로 나오는 개념은 Padding이다. 위와 같이 한 픽셀씩 필터를 이동시킬 경우 단점이 있다.

1. 이미지(feature map)의 사이즈가 줄어든다. 뉴럴 네트워크를 구성할 때, 레이어를 많이 쌓을 수가 없다. 위 예시에서 6x6의 이미지를 3x3의 필터로 단순 convolution할 경우 4x4의 feature map이 생성되었다. 즉, n_out = n_in - filter_size + 1 의 형태다. filter_size가 1보다 클 경우 당연히 이미지가 작아진다.

   ​

2. 이미지 가장자리 부분의 정보 사용량이 적다.

   

   빨간색으로 표시된 픽셀의 경우 필터를 9번 입히게 된다. 초록색으로 표시된 픽셀으 ㅣ경우 필터를 1번밖에 입힐 수 없다.

이러한 단점을 극복하기 위해 적용하는 것이 Padding이다.

이와 같이 이미지 가장자리에 픽셀을 덧붙여주는 것이다. 보통 덧붙여주는 픽셀값은 0으로, 이를 Zero-Padding이라 부른다. 상하좌우로 k개의 픽셀을 덧붙여주며, 이때 k를 padding size라 한다. 그럼 input과 output size의 관계는 아래와 같다.

n_out = n_in - filter_size + 1 + 2 * padding_size

이 때, padding_size = 1/2 (filter_size + 1)로 설정하면 input과 output의 size가 같게 된다.

Stride

필터를 단순히 한 픽셀씩 옆으로 이동시키는 것이 아니라, 중간에 몇 픽셀씩 건너뛸 수도 있다. 이 때 건너뛰는 픽셀의 숫자를 stride라고 부른다. Stride를 1 이상으로 주면 이미지 (feature map) 사이즈를 줄이는 효과가 있다. padding과 stride를 고려한 최종적인 사이즈 계산식은 아래와 같다.

n_out = (n_in - filter_size + 1 + 2 * padding_size) / stride + 1

Convolution on Volume

지금까지의 설명은 2D로 표현되는 흑백 이미지에 대한 설명이었다. RGB 컬러모델이 적용된 이미지는 3차원 텐서로 이루어져 있다(가로 / 세로 / RGB).

위와 같이 2차원 매트릭스가 3겹 있다고 볼 수도 있다. 이 한겹 한겹을 channel이라고 표현한다. 어쨌든 이러한 컬러 이미지를 convolution해주기 위해서는 3차원의 필터가 필요하다. 마찬가지로 3겹의 2차원 매트릭스가 필요하다는 것이다. 즉, convolution을 위해서는 필터의 channel과 이전 레이어의 channel 수가 동일해야한다.

위 이미지와 같은 형태이다. 이 때 convolution 연산은 아래와 같다.

• 각 채널에서 element-wise product를 한다.
• 그럼 27개의 scalar가 나올 것이다. 이를 모두 더해준다.

즉, 3차원의 이미지를 3차원의 필터로 convolution하면 2차원의 매트릭스가 나오는 것이다. 지금까지는 이미지에 한 개의 필터만 적용할 경우에 대해서만 다루었다. 아래 논의는 필터를 여러개 사용할 경우이다.

위 그림은 2개의 필터를 convolution한 경우를 보여준다. 각각의 필터는 2차원 매트릭스를 output으로 갖는다. 따라서 전체 convolution의 output은 이 2개의 매트릭스를 합친 3차원의 텐서가 된다. 개별 필터는 각각 다른 feature를 학습한다. 이를테면 하나는 vertical edge를, 다른 하나는 horizontal edge를 학습할 수 있다.

이제 거의 다 왔다. 약간만 추가하면 하나의 convolution layer가 완성된다.

convolution layer는 위 그림과 같이 구성된다. 빨간색 번호로 표기된 부분을 설명하자면 아래와 같다.

1. 먼저 각각의 필터로 convolution을 취해준다.
2. 각각의 결과 매트릭스에 편향(bias)를 더한다. 편향은 실수 scalar다. 편향을 더한다는 것은, 매트릭스 각각의 element에 같은 실수를 더해준다는 의미다.
3. 2번의 결과에 activation 함수를 적용한다. 위 예시에선 Relu가 사용되었다.
4. activation까지 모든 과정을 거친 4x4x2 사이즈의 output 텐서이다.

지금껏 사용된 notation과 각각의 차원을 정리하자면 아래와 같다. 이해가 되지 않는 부분은 강의를 참고하면 좋을 것 같다.

Pooling

다음으로 설명되는 개념은 pooling이다. feature map의 사이즈를 줄이기 위해 사용된다. 일종의 subsampling 기법이다. Pooling으로 feature map의 사이즈를 줄일 때의 장점은 아래와 같다.

1. computation을 보다 빠르게 수행할 수 있다.
2. 모델이 조금 더 robust해진다.

대표적인 pooling 기법은 max pooling이다.

위 이미지와 같이 이미지의 각 부분 부분에서 값이 가장 큰 것만 뽑는 것이다. 위 사례에서는 filter size = 2, stride = 2가 적용 되었다. max pooling을 통해 4x4의 이미지(feature map)을 2x2의 사이즈로 축소했다. max pooling은 단순히 최고값을 뽑는 과정이기 때문에, 학습시킬 파라미터가 존재하지 않는다.

위 이미지는 5x5 이미지(feature map)에 filter size = 3, stride = 1의 max pooling을 취해준 경우다. pooling이후 이미지 사이즈는 convolution과 마찬가지다.

n_out = (n_in + 2*padding_size - filter_size) / stride + 1

위 그림은 average pooling을 적용한 경우다. 값을 sampling하는 과정에서 max 대신 avg를 취해주었다고 이해할 수 있다.

CNN Example - LeNet

이제 Convolutional layer와 Pooling layer이 무엇인지 알게 되었다. 그럼, 이를 활용해서 뉴럴 네트워크를 어떻게 짤 수 있을까? CNN은 보통 아래와 같이 구성된다.

1. Convolutional Layer

   위에서 쭉 설명한 바와 같다. 이전 레이어에 convolution 및 activation 을 취해주어 feature를 학습하는 역할을 한다.

2. Pooling Layer

   한 개 혹은 여러개의 convolutional layer 뒤에 붙는다. 학습한 feature map을 축소시키는 역할을 한다.

3. Fully Connected Layer (FC)

   가장 단순한 형태의 뉴럴 네트워크 레이어다. Input vector에 Weight를 곱한 뒤 (bias를 더해주고) activation을 취해주는 레이어다. Convolutional Layer를 수 차례 거치면 high-level의 feature들을 갖게 된다. 이 high-level feature들을 활용해서 이미지 분류를 하기 위해 뒷단에 FC를 붙여주는 것이다. 이와 관련된 내용은 여기, FC에 대한 상세한 설명은 여기에서 확인할 수 있다.

   ​

이러한 구조의 CNN을 처음 적용한 모델은 LeNet-5다. 네트워크의 구조는 아래와 같다.

MNIST 데이터셋을 활용하여 손글씨 숫자 이미지를 분류하는 모델이다. 숫자를 분류하므로, class 개수는 10이다. 레이어는 Convolution - Pooling - Convolution - Pooling - (Flatten) - FC - FC - SoftMax로 구성된다. 각각 레이어의 상세 내용은 아래와 같다.

Why Convolution

지금까지 Convolution의 개념과, 기본적인 CNN 네트워크 구조에 대해 살펴보았다. 이 챕터는 ‘Convolution을 왜 쓰는 것일까?’라는 조금 더 근본적인 질문을 던진다. Andrew Ng 교수님(!?)은 FC 레이어와의 비교를 통해 대답한다.

1. Parameter Sharing

   

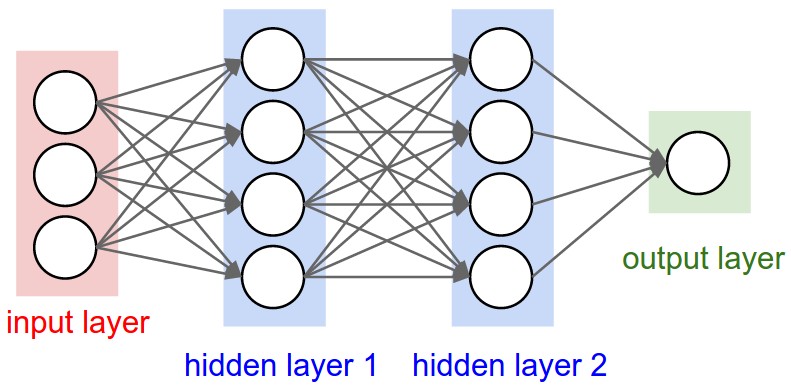
   FC에서는 위와 같이 해당 레이어의 element가 이전 레이어의 모든 element의 가중합계로 구성된다. 따라서 필요한 parameter의 수가 엄청 많다. 반면, Convolution에서, 하나의 필터로 이미지 전체를 훑는다. 즉, 이미지 각 부분 부분은 공통의 parameter를 갖는다고 볼 수 있다. 이를 통해 학습에 필요한 파라미터 수를 줄일 수 있다.

2. Sparcity of connections

   

   FC에서는 해당 레이어의 element가 이전 레이어의 모든 element와 연결된다. 하지만 convolution은 그렇지 않다. 위 그림은 3x3 convolution을 적용한다. 따라서 output 레이어의 하나의 element는 3x3 = 9개의 input element와 연결된다. 즉, convolution을 적용할 경우 FC에 비해 레이어간 연결이 sparse하다.

Parameter Sharing이든 Sparcity of connection이든 필요한 computation 양을 줄이고, 모델의 generalization 능력을 높인다고 해석할 수 있겠다.